(原文刊載於獨立評論@天下)
劉致演博士
劉致演博士
近日一位老師在共同備課會議中提到,她想以代數學之父阿爾花拉子密(al-Khwarizmi)的觀點,從代數及幾何兩個面向引導學生解決以配方法求解二元一次方程式中未知數的問題。如解決等式x2+10x=39問題時,將之視為哪一個數的平方與它自己的10倍之和為39?解題時將x2視為邊長為x的正方形,並於其同側兩邊各加上長寬為x與1之長方形,並補上25個面積為1的正方形,原式左邊即成為邊長為x+5的正方形,由於右式根據等量公理同加25的結果即成為邊長為8的正方形,此時即知x+5等於8,而x的值即為3。
由於學生在實際操作時,多半以代數方法解決配方法求解二元一次方程式的未知數,於是共同參與備課的老師們都希望能了解為什麼要這樣做?
「我希望他們知道,解決問題不是只有一種方法。以配方法為例,可以交替使用具象跟代數的方法。很多學生到最後都只會背公式,如常數項就是x項係數一半的平方,然後他們就很制式的一直算、一直算,當x平方項不是1的時候他們就卡住了。」
美國國家研究會(National Research Council)主張,學生能使用流暢的數學程序,是達成數學學習理解的表徵之一,即瞭解並能彈性、準確而有效率地、合適地運用數學程序性知識。由於學生對於特定數學知識的程序性與概念性理解兩者互為表裡,因此會讓老師與家長誤以為透過大量練習學生就能學好數學,因為「熟能生巧」是大家早已熟知的道理,但事實上學生「知其然」並不表示也能「知其所以然」。
很多老師以「題海戰術」讓學生透過大量練習來考出好成績,學生因為重複練習相同類型的題目,到最後都能「直覺」的寫出答案,換句話說寫數學題如同反射動作,不經思索即能解出答案;其次,由大部分的國中數學段考題目(甚至是會考)都是選擇題,選對答案就能考高分,孩子怎會思考同一個問題可能有不同的解題策略?遑論分析不同的表述式或解題策略背後所蘊含的意義。如是,孩子學習數學的目的究竟是為了什麼?
了解數學本質,才能看見不同方法
英國華威大學(Warwick University)數學思考榮譽教授高大衛(David Tall)在其著作《人類如何學會數學思考:探索數學的三個世界》(How humans learn to thinking mathematically: Exploring the three worlds of mathematics)中指出,人類數學學習發展以具象(embodiment)、符號(symbolism)與公理(formalism)等數學的三個世界為基礎。簡單來說,「具象世界」是我們藉由真實世界的物件(objects)將感官經驗加以轉化成抽象化的數學語言;「符號世界」則是我們將具象世界的過程或概念透過心智壓縮化約成符號,讓我們能夠以簡潔的方式進行數學思考;「形式化」世界則純粹以數學性質藉由形式化的定理證明來論述數學本質。
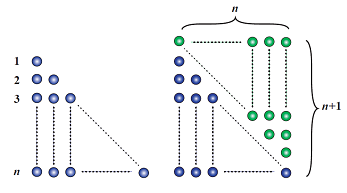
以求解1+2+3…+n=?(n為正整數)為例(此即我們熟知的自然數求和公式或梯形公式),我們可以用具象方法(如下圖)得到1/2 n(n+1)的結果,我們亦可已透過符號化的方式將1+2+3…+n重新書寫成n+…+3+2+1,將兩級數和的每一項個別相加,得結果為n個(n+1),其和為n(n+1),則所求為n(n+1)的二分之一,即1/2 n(n+1);甚至,我們可以數學歸納法(形式化)來證明該公式的真確性。
孩子隨著對於數學本質及內容了解與深入,針對相同數學問題就能提出不同解題策略與方法;例如求解複數5+12i的平方根,可令其平方根為a+bi並將之平方後進行比較係數,或是透過高斯平面並結合向量概念亦可求得相同答案;另如德國數學家約翰.米勒(Johannes Müller)亦稱為雷吉蒙塔努斯(Regiomontanus),在西元1471年提出一著名的極限問題:「牆上掛了一幅畫,有一個人站在畫前,眼睛與畫作上緣及下緣(在該人眼睛之上)所形成的角度稱為視角,請問此人站在何處時,其視角最大?」;解題時必須找出眼睛與畫作的上緣及下緣的關係並將之具象化,透過圓之切割線性質或三角正切函數,甚或微積分都能解出此問題的最佳解。
學數學,也學到解決問題的能力
數學學習的目的就是為提升孩子解決問題的能力,並針對往後生活中沒有標準答案與解題方法的問題做準備,有鑒於此,數學其實是培養孩子「創意思考」與「批判思考」等心智習性之極佳工具。美國白宮科技創新顧問及《未來產業》一書作者亞歷克.羅斯(Alec Ross)認為,「解決問題」、「創新創造力」與「學習如何思考」是迎向未來世界之必備能力。
在教學現場裡,其實有很多老師是為了培養學生「帶得走的能力」而努力,但美中不足的是,當前考試制度主要並非評量學生所習得的能力。因此,教學方法改革,評量方法及看待孩子學習成就的觀點也應該跟著與時俱進;如果你是老師,你希望了解學生已經知道多少「事實」,還是習得多少「能力」?學生出社會後,如果你是老闆,你希望員工記得多少書本內容,還是他有能力做什麼?答案顯然顯而易見。
由於學生在實際操作時,多半以代數方法解決配方法求解二元一次方程式的未知數,於是共同參與備課的老師們都希望能了解為什麼要這樣做?
「我希望他們知道,解決問題不是只有一種方法。以配方法為例,可以交替使用具象跟代數的方法。很多學生到最後都只會背公式,如常數項就是x項係數一半的平方,然後他們就很制式的一直算、一直算,當x平方項不是1的時候他們就卡住了。」
美國國家研究會(National Research Council)主張,學生能使用流暢的數學程序,是達成數學學習理解的表徵之一,即瞭解並能彈性、準確而有效率地、合適地運用數學程序性知識。由於學生對於特定數學知識的程序性與概念性理解兩者互為表裡,因此會讓老師與家長誤以為透過大量練習學生就能學好數學,因為「熟能生巧」是大家早已熟知的道理,但事實上學生「知其然」並不表示也能「知其所以然」。
很多老師以「題海戰術」讓學生透過大量練習來考出好成績,學生因為重複練習相同類型的題目,到最後都能「直覺」的寫出答案,換句話說寫數學題如同反射動作,不經思索即能解出答案;其次,由大部分的國中數學段考題目(甚至是會考)都是選擇題,選對答案就能考高分,孩子怎會思考同一個問題可能有不同的解題策略?遑論分析不同的表述式或解題策略背後所蘊含的意義。如是,孩子學習數學的目的究竟是為了什麼?
了解數學本質,才能看見不同方法
英國華威大學(Warwick University)數學思考榮譽教授高大衛(David Tall)在其著作《人類如何學會數學思考:探索數學的三個世界》(How humans learn to thinking mathematically: Exploring the three worlds of mathematics)中指出,人類數學學習發展以具象(embodiment)、符號(symbolism)與公理(formalism)等數學的三個世界為基礎。簡單來說,「具象世界」是我們藉由真實世界的物件(objects)將感官經驗加以轉化成抽象化的數學語言;「符號世界」則是我們將具象世界的過程或概念透過心智壓縮化約成符號,讓我們能夠以簡潔的方式進行數學思考;「形式化」世界則純粹以數學性質藉由形式化的定理證明來論述數學本質。
以求解1+2+3…+n=?(n為正整數)為例(此即我們熟知的自然數求和公式或梯形公式),我們可以用具象方法(如下圖)得到1/2 n(n+1)的結果,我們亦可已透過符號化的方式將1+2+3…+n重新書寫成n+…+3+2+1,將兩級數和的每一項個別相加,得結果為n個(n+1),其和為n(n+1),則所求為n(n+1)的二分之一,即1/2 n(n+1);甚至,我們可以數學歸納法(形式化)來證明該公式的真確性。

孩子隨著對於數學本質及內容了解與深入,針對相同數學問題就能提出不同解題策略與方法;例如求解複數5+12i的平方根,可令其平方根為a+bi並將之平方後進行比較係數,或是透過高斯平面並結合向量概念亦可求得相同答案;另如德國數學家約翰.米勒(Johannes Müller)亦稱為雷吉蒙塔努斯(Regiomontanus),在西元1471年提出一著名的極限問題:「牆上掛了一幅畫,有一個人站在畫前,眼睛與畫作上緣及下緣(在該人眼睛之上)所形成的角度稱為視角,請問此人站在何處時,其視角最大?」;解題時必須找出眼睛與畫作的上緣及下緣的關係並將之具象化,透過圓之切割線性質或三角正切函數,甚或微積分都能解出此問題的最佳解。
學數學,也學到解決問題的能力
數學學習的目的就是為提升孩子解決問題的能力,並針對往後生活中沒有標準答案與解題方法的問題做準備,有鑒於此,數學其實是培養孩子「創意思考」與「批判思考」等心智習性之極佳工具。美國白宮科技創新顧問及《未來產業》一書作者亞歷克.羅斯(Alec Ross)認為,「解決問題」、「創新創造力」與「學習如何思考」是迎向未來世界之必備能力。
在教學現場裡,其實有很多老師是為了培養學生「帶得走的能力」而努力,但美中不足的是,當前考試制度主要並非評量學生所習得的能力。因此,教學方法改革,評量方法及看待孩子學習成就的觀點也應該跟著與時俱進;如果你是老師,你希望了解學生已經知道多少「事實」,還是習得多少「能力」?學生出社會後,如果你是老闆,你希望員工記得多少書本內容,還是他有能力做什麼?答案顯然顯而易見。
